写在前面 ：

作为一个初学的弱渣，写这篇东西完全是在当笔记做。

我觉得我们这门课虽然叫Operating System Concepts,到不如说是安全基本知识入门（所以学啥完全取决于老师的方向和自己）。这部分大概预习了（雾。。）有一周，还是懵懂，不对的地方希望大家多多指教。课本用得是很经典的Abraham Sliberschatz，Peter Bear Galvin 和Greg Gagne 的 Operating System Concepts 9th Edition（也就是恐龙书）. （然而弱渣的我基本上是看中译第七版，翻译得一塌糊涂）刚好看到知乎最近也在升级Https，感觉没有很好的答案去解释这些概念，所以就把自己在书上看到的记在这里。

中文是我自己翻译的，不对准确性负责 ，自己的陋见用的是斜体。（时间有限，所以就选一部分啦，请参见原书Chapter 15。）

版权归书籍原作者所有。

Encryption 加密

Because it solves a wide variety of communication security problems, encryption
is used frequently in many aspects of modern computing. It is used to send
messages securely across a network, as well as to protect database data,
files, and even entire disks from having their contents read by unauthorized
entities.
由于加密能解决很多通信领域的安全问题，它被广泛使用在现代计算的很多方面，包括在不同的网络间安全地发送消息以及避免数
据，文件乃至整个磁盘的内容被不合法的实体读取。

所以加密是用来解决安全问题的一种手段，关于 安全问题 ，前面一小节有提过：

Security, on the other hand, requires not only an adequate protection
system but also consideration of the external environment within which the
system operates.

也就是说安全既要考虑内部的保护问题（简单的说就是系统内部的访问权限控制）也要考虑系统外部环境的操作。反过来对系统的攻击（attack）集中在：

Breach of confidentiality（保密性）,

Breach of integrity（完整性）,

Breach of availability（可用性，简单的说就是unauthorized destruction未被许可的破坏）,

Theft of service（偷窃服务, 即 unauthorized use of resources私自占有使用资源）,

Denial of service（拒绝服务）.

回到 加密 这个话题，

An encryption algorithm enables the sender of a message to ensure that only a computer possessing a certain key can read the message, or ensure that the writer of data is the only reader of that data.
加密算法能够让一个消息的发送者确定只有那些拥有特定密钥的计算机能够读取这个消息，或者仅仅只有数据的写入者才能读取它。

An encryption algorithm consists of the following components:

• A set K of keys.
• A set M of messages.
• A set C of ciphertexts.
• An encrypting function E : K → (M→C). That is, for each k ∈ K, E_k is a
  function for generating ciphertexts from messages. Both E and E_k for any k
  should be efficiently computable functions. Generally, E_k is a randomized
  mapping from messages to ciphertexts.

• A decrypting function D : K → (C → M). That is, for each k ∈ K, D_k is a
  function for generating messages from ciphertexts. Both D and D_k for any
  k should be efficiently computable functions.

  加密算法由下面部分构成：

  • 一个密钥集合K

  • 一个消息集合M

  • 一个密文集合C

  • 一个加密函数 E : K → (M→C). 即，对于每个密钥 k ∈ K, E_k是一个用消息生成密文的函数。对任意k来说， E 和 E_k都是高效的且可计算的函数。大致来说，E_k 是从消息到密文的一个随机映射。

  • 一个解密函数 E : K → (C→M). 即，对于每个密钥 k ∈ K, D_k是一个用密文生成消息的函数。对任意k来说， D 和 D_k都是高效的且可计算的函数。大致来说，D_k是从密文到消息的一个随机映射。

An encryption algorithm must provide this essential property: given a
ciphertext c ∈ C, a computer can compute m such that E_k (m) = c only if
it possesses k. Thus, a computer holding k can decrypt ciphertexts to the
plaintexts used to produce them, but a computer not holding k cannot decrypt
ciphertexts. Since ciphertexts are generally exposed (for example, sent on a
network), it is important that it be infeasible to derive k from the ciphertexts.
There are two main types of encryption algorithms: symmetric and
asymmetric.
一个加密算法必须提供这个必要属性：给定一个密文c ∈ 密文集合C， 只有计算机掌握k的时候才能通过计算加密函数E_k (m) = c得到消息m。 因此，只有掌握密钥k的计算机可以解密密文，但是没有掌握k的计算机却不可以。因为密文常常是被暴露出来的（比如在网络中发送的时候），所以很重要的一点是让从密文推出密钥k变得不可能。一共有两种加密：对称加密和非对称加密。

Symmetric encryption algorithm and Asymmetric encryption algorithm

对称加密：

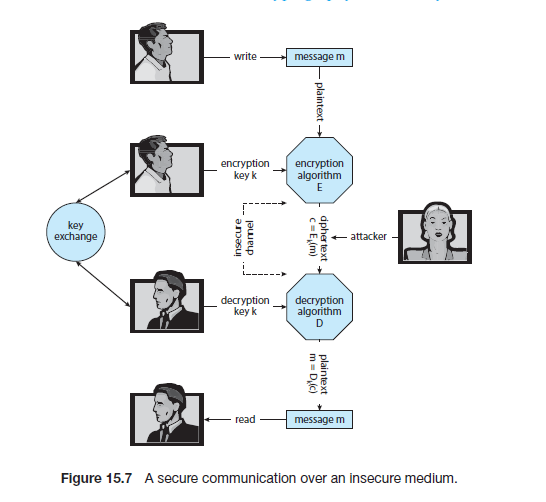
In a symmetric encryption algorithm, the same key is used to encrypt and to
decrypt. Therefore, the secrecy of k must be protected.
对称加密算法使用同样的密钥来加密和解密，因此，必须使密钥k保持机密。

该图展示了用对称密钥加密的过程。

几种对称加密算法：

data-encryption standard (DES)：64-bit value,a 56-bit key, performing a series of transformations that are based on substitution and permutation operations （基于替换和排列变换）. Work on a block of bits at a time, is known as a block cipher.

triple DES: DES algorithm is repeated three times (two encryptions and one decryption) on the same plaintext using two or three keys—for example, c = E_k3 (D_k2 (E_k1 (m))). When three keys are used, the effective key length is 168 bits (i.e. 56*3).

advanced encryption standard (AES)：another block cipher, use key lengths of 128, 192, or 256 bits and works on 128-bit blocks. 这里block cipher应该是按照固定bit长度加密的意思

RC4: stream cipher based (encrypt and decrypt a stream of bytes or bits rather than a block). This is useful when the length of a communication would make a block cipher
too slow.

非对称加密：

In an asymmetric encryption algorithm, there are different encryption and
decryption keys…. Any sender can use that key to encrypt a communication,
but only the key creator can decrypt the communication. This scheme, known
as public-key encryption, was a breakthrough in cryptography.
在非对称加密算法，加密和解密密钥是不同的。…任何发送者能均够能使用那个密钥 （即公钥）加密通讯，但是只有密匙创建者能解密通讯。这种模式，被称为公钥加密，曾是密码学的一个突破。

Example: RSA Algorithm 举例：RSA 加密算法

In RSA, k_e is the public key, and k_d is the private key. N is the product of
two large, randomly chosen prime numbers p and q (for example, p and q are
512 bits each). It must be computationally infeasible to derive k_d,N from k_e,N , so
that k_e need not be kept secret and can be widely disseminated. The encryption
algorithm is E_ke ,N(m) = mk_e mod N, where k_e satisfies k_e k_d mod (p−1)(q−1) =1. The decryption algorithm is then D_kd ,N(c) = ck_d mod N.

在RSA中，k_e 是公钥，k_d 是私钥, N是两个较大的随机选择的素数之积（比如，p,q每个都是512位长）。从k_d,N 到k_e,N 一定是不能计算出的,因此k_e 不必保持机密并可以被广泛传播。

加密算法是E_ke , N(m) = m^k_e mod N,k_e 满足 k_e k_d mod (p−1)(q−1) = 1.

接着解密算法是 D_kd ，N(c) = c^k_dmod N

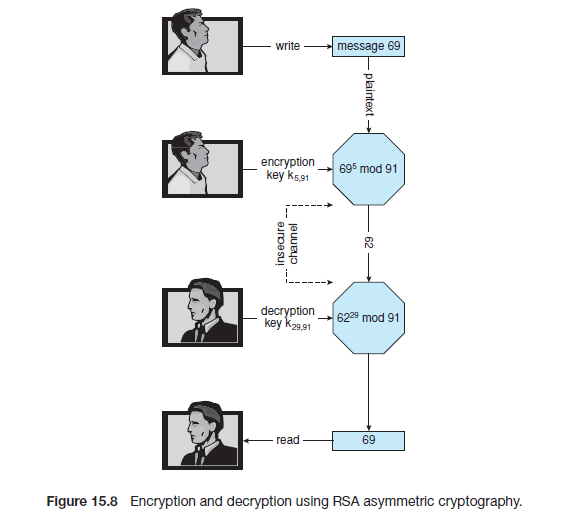
An example using small values is shown in Figure 15.8. In this example, we
make p = 7 and q = 13.We then calculate N = 7∗13 = 91 and (p−1)(q−1) = 72.
We next select k_e relatively prime to 72 and < 72, yielding 5. Finally, we calculate
k_d such that k_e k_d mod 72 = 1, yielding 29. We now have our keys: the public
key, k_e ,N = 5, 91, and the private key, k_d ,N = 29, 91. Encrypting the message 69
with the public key results in the message 62, which is then decoded by the
receiver via the private key.

图15.8一个比较小一点的例子。我们让 p = 7, q =13。然后计算N = 7*13 且 (p−1)(q−1) = 72。接着我们相应的给k_e选择一个小于72的素数，得到5。最后我们通过k_e k_d mod 72=1计算得到 k_d ，为29。因此现在k_e,N = 5, 91；私钥 k_d ,N = 29, 91。用公钥加密消息69得到密文结果62,然后通过私钥解密。

RSA 算法： 数学知识

关于RSA算法用到的数学知识，请参见阮一峰大神的教程I(前置数学知识)
及
阮一峰大神的教程II（最后一部分:算法正确性的证明)

The use of asymmetric encryption begins with the publication of the public
key of the destination. For bidirectional communication, the source also must
publish its public key. “Publication” can be as simple as handing over an
electronic copy of the key, or it can be more complex. The private key (or “secret
key”) must be zealously guarded, as anyone holding that key can decrypt any
message created by the matching public key.

非对称加密的使用从公钥的发布开始。对于双向通信，消息源还必须发布它的公钥 （译者注：注意直接把公钥发布出去会出问题，下面会提到）。发布可以简单的像传递这个公钥的电子拷贝一样，也可以使得它变得更复杂一点。私钥必须被积极保护起来。因为任何持有这个私钥的人，都可以解密由和这个私钥相匹配的那个公钥加密的任何信息。

We should note that the seemingly small difference in key use between
asymmetric and symmetric cryptography is quite large in practice. Asymmetric
cryptography is much more computationally expensive to execute. It is much
faster for a computer to encode and decode ciphertext by using the usual
symmetric algorithms than by using asymmetric algorithms. Why, then, use
an asymmetric algorithm? In truth, these algorithms are not used for general purpose
encryption of large amounts of data. However, they are used not
only for encryption of small amounts of data but also for authentication,
confidentiality, and key distribution, as we show in the following sections.

我们应该注意到非对称加密和对称加密在密钥使用上的微小不同其实导致在实践中二者的差别是非常大的。非对称加密计算会消耗更多的资源。通常来说，使用对称加密和解密密文比非对称加密密文更快。那么为啥我们还要用非对称加密算法呢？事实上，这些（非对称加密）算法不是为通常意义上大量数据的加密而准备的。非对称加密不仅仅被使用在少量数据的加密中也被使用在验证，保密和密钥分发的过程，就像下面几个小节所述的一样。

Authentication认证

We have seen that encryption offers a way of constraining the set of possible
receivers of a message. Constraining the set of potential senders of a message
is called authentication. Authentication is thus complementary to encryption.

加密可以提供一种限制信息接受者范围的途径（译者注：即有密钥(非对称中是私钥)才能解密没有则不能）。限制信息的发送者范围叫做验证。验证是加密的补充。

Authentication is also useful for proving that a message has not been modified.

验证也能确保信息不被更改。

An authentication algorithm using symmetric keys consists of the following components:

• A set K of keys.

• A set M of messages.

• A set A of authenticators.

• A function S : K → (M → A). That is, for each k ∈ K, S_k is a function for
  generating authenticators from messages. Both S and S_k for any k should
  be efficiently computable functions.

• A function V : K → (M×A→{true, false}). That is, for each k ∈ K, V_k
  is a function for verifying authenticators on messages. Both V and V_k for
  any k should be efficiently computable functions.

使用对称密钥的认证算法由下面的部分构成：

• 一个密钥集合K

• 一个消息集合M

• 一个验证器集合A

• 一个验证器生成函数 S : K → (M→A). 即，对于每个密钥 k ∈ K, S_k 是一个用消息生成验证器的函数。对任意k来说， S和S_k 都是高效的且可计算的函数。

• 一个验证器验证函数 E : K → (M×A→{true, false}). 即，对于每个密钥 k ∈ K, V_k 是一个用来验证特定消息的验证器的函数。对任意k来说， V 和V_k 都是高效的且可计算的函数。

The critical property that an authentication algorithm must possess is this:
for a message m, a computer can generate an authenticator a ∈ A such
that V_k (m, a) = true only if it possesses k. Thus, a computer holding k can generate authenticators on messages so that any computer possessing k can
verify them. However, a computer not holding k cannot generate authenticators
on messages that can be verified using V_k . Since authenticators are generally
exposed (for example, sent on a network with the messages themselves), it
must not be feasible to derive k from the authenticators. Practically, if V_k (m, a)
= true, then we know that m has not been modified, and that the sender of
the message has k. If we share k with only one entity, then we know that the
message originated from k.

验证算法的重要属性是：对一个消息m,只有计算机掌握k的时候可以生成一个验证器 a ∈ A 使得验证函数 V_k (m, a) = true 。 因此，任何持有密钥k的计算机可以生成关于消息m的验证器，这个验证器可被其它任意一台任何持有密钥k的计算机通过V_k 来验证。因为验证器通常是被暴露的（比如，在网络上和消息一起被发送），所以很重要的一点是让从验证器推出密钥k变得不可能。实际上，如果V_k (m, a) = true,我们就可以知道消息没被更改过。如果我们只把k分享给过一个实体，那么我们就能知道消息源自最初的发布者。

Just as there are two types of encryption algorithms, there are two main varieties of authentication algorithms.

和两种加密算法相同，也有两种认证算法。

Hash函数

The first step in understanding these algorithms is to explore hash functions. A hash function H(m) creates a small, fixed-sized block of data, known as a message digest or hash value, from a message m. Hash functions work by taking a message, splitting it into blocks, and processing the blocks to produce an n-bit hash. H must be collision resistant —that is, it must be infeasible to find an m^‘ = m such that H(m) = H(m^‘ ). Now, if H(m) = H(m^‘ ), we know that m = m^‘ — that is, we know that the message has not been modified. Common message-digest functions include MD5, now considered insecure, which produces a 128-bit hash, and SHA-1, which outputs a 160-bit hash. Message digests are useful for detecting changed messages but are not useful as authenticators. For example, H(m) can be sent along with a
message; but if H is known, then someone could modify m to m^‘ and recompute H(m^‘ ), and the message modification would not be detected. Therefore, we must authenticate H(m).

理解这两种算法的第一步是探索hash函数。hash函数H(m)用一条消息创建一块小的且固定大小的数据，被称作消息摘要或者hash值。它是这样工作的：取一条消息,将其拆分成块，并且处理这些小块来产生n位的hash。H函数是拒绝碰撞的，也就是说，如果m^‘ =m，则H(m) = H(m^‘ ) 是不成立的。所以现在，如果H(m) = H(m^‘ ), 那么一定有m = m^‘ ，也就是说，我们可以确定这条消息m没有被更改。常见的消息摘要函数包括产生128位hash摘要的MD5（现在已经被认为是不安全的）和产生160位hash摘要的SHA-1。消息摘要对检测消息是否被更改十分有用但是对验证验证器来说是没用的。比如，H(m)可以和一条消息一起被发送，但是如果H函数是已知的其他人可以将m修改成m^‘ 然后重新计算H(m^‘ ),并且这种更改不能被检测出来。因此，我们必须验证H(m).

message-authentication code (MAC)消息验证码

• uses symmetric encryption 使用对称加密

• a cryptographic checksum is generated from the message using a secret key 消息的加密校验和通过一个密钥来被生成。

• k is needed to compute both S_k andV_k , so anyone able to compute one can compute the other. k用来计算S_k 和V_k ,所以任何能计算一个的人也能计算另外一个。

digital-signature algorithm数字签名算法

• the authenticators thus produced are called digital signatures 这种算法的验证器也被叫做数字签名。

• Digital signatures are very useful in that they enable anyone to verify the authenticity of the message.数字签名使得任何人可以验证消息的真实性。

• k_v is the public key, and k_s is the private key. k_v 是公钥，k_s 是私钥。

• infeasible to derive k_s from k_v 不可从k_v 推导出k_s

• Example: RSA digital-signature algorithm ，similar to the RSA encryption algorithm, but the key use is reversed. The digital signature of a message is derived by computing S_ks (m) = H(m)^k_s mod N.The key k_s again is a pair <d, N>, where N is the product of two large, randomly chosen prime numbers p and q. The verification algorithm is then
  V_kv = ? ( a^k_v mod N = H(m)), where k_v satisfies k_v k_s mod (p − 1)(q − 1) = 1.

• 例子：RSA 数字签名算法, 和RSA加密算法类似，但是key的使用是相反的(译者注：即私钥算出验证器，公钥验证验证器)。一个消息的数字签名S_ks (m)是通过计算S_ks (m) =H(m)^k_s mod N 得到的。密钥k_s 同样是有序数对<d,N>,N同样是两个巨大的且随机选出的素数p和q之积。验证算法是V_kv = ? ( a^k_v mod N =H(m)),同样k_v 满足k_v k_s mod (p − 1)(q − 1) = 1.

（先写到这里好了，时间有限，回来将后面SSL的部分补上。）

留言: